古建筑榫卯抗震性能研究进展

中国木结构古代建筑因其独特的建筑形式与结构性能而著称于世，并影响了日本、韩国和越南等临近国家，是中华乃至世界文明的重要组成部分。经过不断的发展和演变，不同时期对木结构古建筑各组成部分的构造、尺度等都有相对成熟的规定，如宋代的《营造法式》，清代的《工程做法则例》和成书于民国时期的《营造法原》等等。以上不同时期工程做法之间既有继承，又有发展，体现了安全与美观的结合。但由于科技水平的限制，对于各种结构做法，并没有一个从现代力学角度出发的科学阐释。

我国木结构古代建筑的一个重要特征在于结构构架采用榫卯连接。所谓榫卯连接是将梁端做成榫头形式，将柱身做成卯口形式，将榫头插入卯口中，从而形成的一种凹凸结合的特殊连接体系［1］。一般认为，这种构件的连接方式，使得中国传统的木结构建筑成为超越了当代建筑排架、框架或者钢架的特殊柔性结构体，不但可以承受较大的荷载，而且允许产生一定的变形，在地震荷载下通过变形吸收地震能量，减小结构的地震响应［2 －5］。

随着使用年限的增长，现存木结构古代建筑中木材材性不断退化，各种自然和人为因素也降低了节点的力学性能［6 －9］，威胁结构的安全。因此，开展榫卯节点抗震性能研究，对于准确分析中国木结构古代建筑结构的抗震性能，提出科学合理的保护措施具有十分重要的意义。

近20年来，工程结构和力学专家结合对具体古建筑的抢修工程，将现代试验检测方法，力学理论和数值分析方法引入到木结构古建筑研究中，开展榫卯节点力学行为和结构抗震性能分析，使古建筑结构研究进入了一个新的阶段。本文将对中国古代建筑榫卯节点抗震性能研究进展情况进行梳理，并对其未来的发展方向进行讨论。

古建筑榫卯连接有多种形式，形态各异，其种类划分不仅与榫卯的功能有关，还与木构件所处的位置，构件之间的组合角度，结合方式等有直接关系。如柱根、童柱、瓜柱与梁架相交部位采用的管脚榫；额枋、顺梁、 金枋等与柱相交部位采用的燕尾榫；梁、柱相交部位采用的馒头榫；以及透榫、半榫、十字卡腰榫、十字刻半榫等等。这其中，最常用于梁柱构件“构木成架”的典型节点连接形式有直榫和燕尾榫两种，根据直榫是否穿透卯构件又细分为透榫和半榫。直榫，榫头无明显宽度变化，一般用于水平向安装，见图1 (a) 所示；燕尾榫榫头端部宽，根部窄，呈燕尾状，一般用于竖向安装，如图1 (b) 所示。一般认为，榫卯节点这种完全区别于现代结构的特殊构造，是使木结构古建筑获得较高抗震性能的原因之一［10 －12］。国内许多学者分别进行了大量燕尾榫节点和直榫 ( 透榫和半榫) 节点的低周往复加载试验，对榫节点的工作机制、滞回性能和破坏模式等进行了详细的分析。

图1两种典型的榫卯节点示意图

榫卯节点的滞回曲线特征

高大峰和赵鸿铁等［13 －14］较早通过对宋式木构架1：3. 52缩尺模型的水平反复加载试验，研究了燕尾榫节点的受力特征和工作机制，认为榫卯节点的破坏特征表现为榫卯间的相互挤压变形使榫头和卯口间的咬合作用削弱，最终导致榫头从卯口中拔出而使结构丧失承载能力。在整个加载过程中，节点对梁柱构件的约束较弱，因而整个构架变形主要表现为节点的转动，外观上看不出明显的梁柱轴线弯曲变形。

姚侃等［15］和赵鸿铁等［16 －17］对直榫和燕尾榫节点进行拟静力试验，获取了典型榫卯节点的滞回曲线 (见图2) ，并对其滞回性能进行了分析。在外荷载的反复作用下，榫卯节点的一般过程可分为初始滑移、弹性变形和破坏等3个过程。在加载初期，榫卯接合处在力的作用下由松弛状态开始挤紧，有明显的滑移产生，节点耗能能力较弱。随着构架侧移增大，榫头与卯口相对转角增大，榫卯连接被挤紧而密合，节点耗能能力增强，木构架在屈服前的弹性阶段，滞回环形状外鼓，曲线基本为直线，此时构架承载力由榫卯节点提供。随着控制侧移继续增大，榫卯脱出闭合的长度加大，表征刚度变化的滞回曲线的斜率逐渐下降，表明榫卯刚度有所降低。

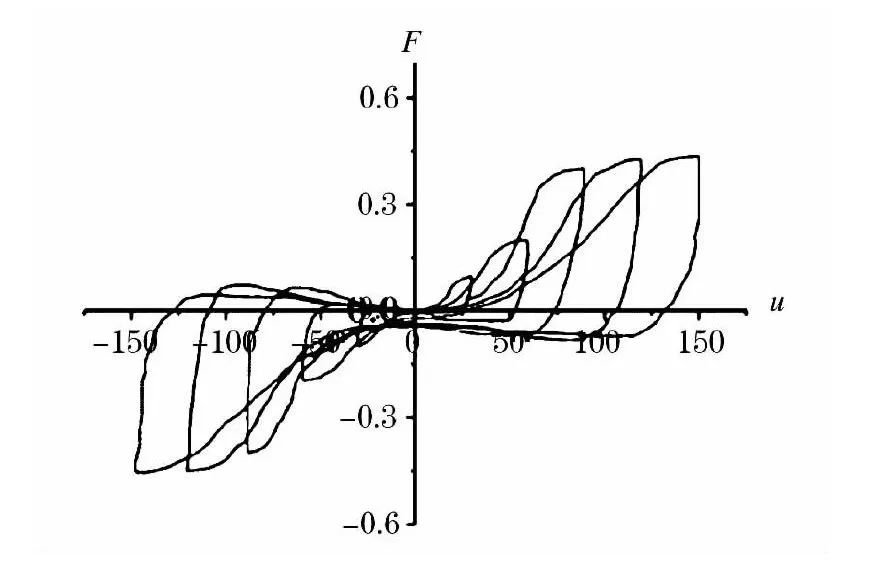
图 2 典型的榫卯节点滞回曲线

榫卯连接的弯矩- 转角滞回曲线大致为反“Z”型，具有明显的“捏拢”效应。整个阶段的变形过程表现出明显的变刚度特征，其刚度变化过程为：初始弹性阶段，表现为较大刚度；变形增加阶段，滞回曲线的斜率降低较快，刚度退化明显，而且发展速度很快；破坏阶段，节点失去抵抗弯矩能力而破坏。在变形过程中，榫卯之间在受力过程中发生了较大的剪切变形和滑移变形，且滑移量随位移幅值的增加而增大［18 －20］。

徐明刚等［21］、李佳伟等［22］以半榫、透榫和燕尾榫为对象，通过对比不同榫卯节点的最大转动刚度及弯矩值，得出如下结论：对于同一种榫卯节点，榫头越长其抗弯承载力越强；节点抗弯强度：透榫> 燕尾榫> 半榫；节点残余强度：透榫> 燕尾榫> 半榫。

周乾等［23 －24］发现当构架达到控制位移时卸载，变形并不能恢复，必须反向加载才能实现，这说明榫卯节点的恢复力较小，构架的塑性变形需要外力恢复。

各课题组获取的滞回曲线环的均表现出了比较饱满的特征，尤其是屈服以后面积扩大很快，表明试件能量耗散较大，其原因在于由于构架侧移增大时，榫卯之间产生较大的滑移摩擦，同时又是一个榫卯挤紧而产生塑性变形的过程，表现出较好的耗能能力。

文献[23]采用计算相对变形的办法表征节点延性，得出榫卯节点的相对变形值介于0. 462 ~0. 567之间，均值为0. 505，远大于反映混凝土结构延性的节点的相对变形值，反映了榫卯节点有较好的变形能力和延性。但是由于木材个性异性，以及加工误差等原因，计算结果有较大的离散性。

榫卯节点的恢复力模型

恢复力模型是根据大量从试验中获得的恢复力与变形的关系曲线经适当抽象和简化而得到的实用数学模型，是结构抗震性能在结构弹塑性地震反应分析中的具体体现［25 －26］。

文献[15]根据骨架曲线的变刚度特性和卸载阶段的滑移特性构造出恢复力模型。该模型从总体上划分为加载、卸载和再加载3个阶段。加载阶段节点的恢复力特性可用三折线表征，分别代表榫卯挤紧的初始滑移段，挤紧后至屈服的强化段，和屈服后的极限荷载的第3阶段 (见图3) 。各段刚度间的关系为K₂= 4H137K₂，K₂= 0. 407K₂。卸载阶段为斜率等于K₂的斜直线，每历经一个加载过程之后再加载时滑移量增加，但榫卯再次挤紧，刚度在加强后会沿与K₂斜率平行的方向发展。再加载阶段以某方向卸载至弯矩为零时的残余变形为起点向反方向加载，与上一个循环的最高点直线相连。如果该点超过屈服点，则与此特征点相连，再沿骨架曲线前进。

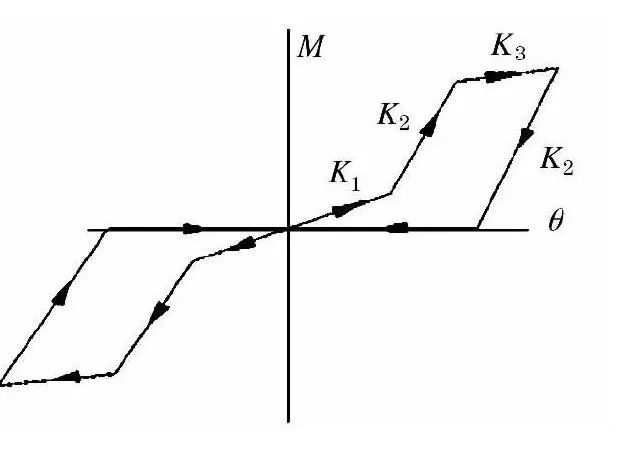
图3榫卯节点恢复力模型1

文献[2]分析认为，在地震持续反复作用之下，榫卯节点主要表现为滑移变形、弹塑性变形，榫、卯连接松动、柔性化，卯口劈裂，以至于脱卯等基本破坏特征，并据此将榫卯节点的加载过程细分为滑移阶段，弹性阶段，塑性发展阶段和破坏阶段四个阶段，构造了恢复力模型 (见图4) 。

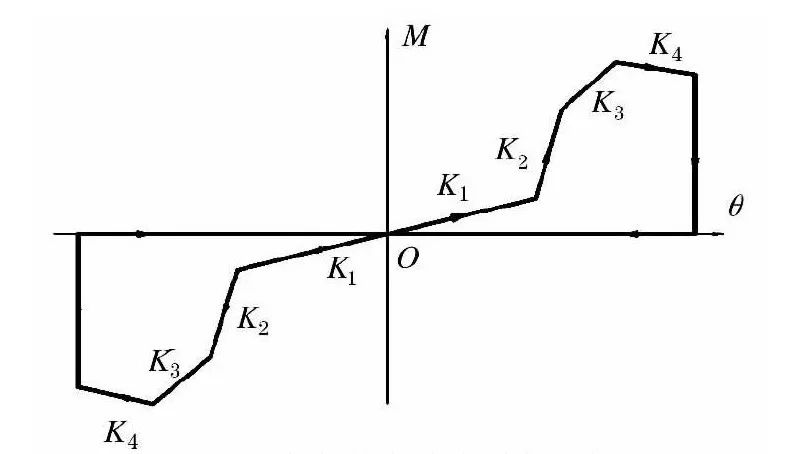
图4榫卯节点恢复力模型2 

文献[21 -22]将加载过程划分为榫卯有松弛开始挤紧阶段，榫卯之间相互滑移耗能阶段和榫卯节点由屈服阶段进入极限阶段，并认为在卸载后变形恢复到0的过程中，节点弯矩亦可恢复到零，构建了恢复力模型 (见图5) 。基于对试验数据分析，模型中各刚度取值为K₁= 3. 602 ( kN·m) / rad，K₂= 5. 755 ( kN·m) / rad，K₃= 1. 781 ( kN·m) / rad。

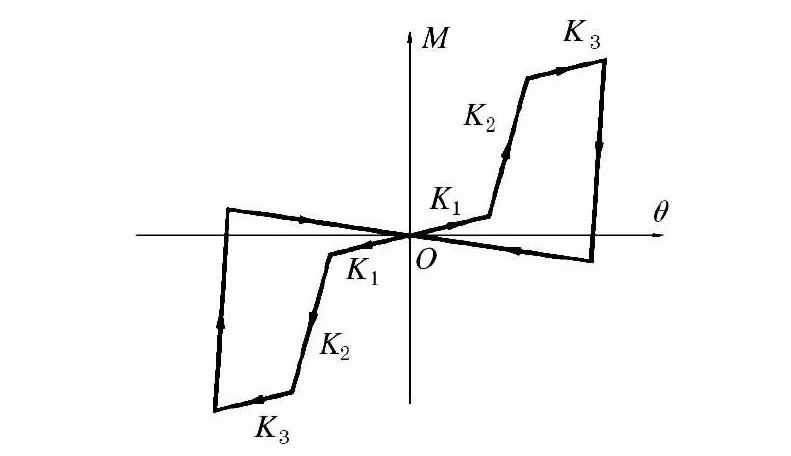
图5榫卯节点恢复力模型3 

赵鸿铁等［16 －17］和隋龑等［20］认为初始加载时节点不会产生滑移现象，只有在经过初始加载以后，节点发生松动，才会产生滑移- 挤紧的过程，同时考虑到节点卸载后有抵抗负弯矩的能力，构造出了恢复力模型 (见图6) ，该恢复力模型可表示为：

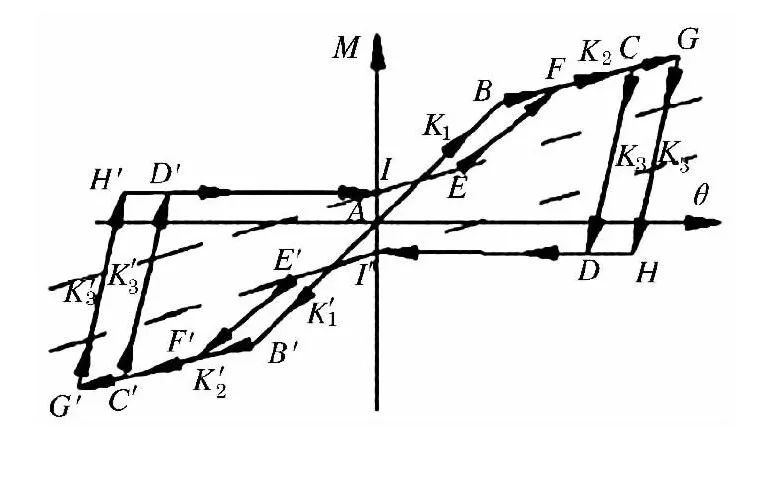
图6榫卯节点恢复力模型4 

根据该模型特征，划分不同阶段的刚度分别为初始连接刚度K₁，滑移退化后刚度K₂，卸载刚度K₃和K₄卸载滑移刚度根据试验结果，K₄可近似取为0，考虑到燕尾榫和透榫的差异，不同形式榫卯节点其它各阶段刚度分别按照表1取值。

对于加载阶段的M - θ 关系，文献[16 - 17]还分别针对燕尾榫节点和透榫节点试验结果，拟合出S形M - θ 关系曲线。

表 1 节点特征刚度取值

kN·m·rad－ 1

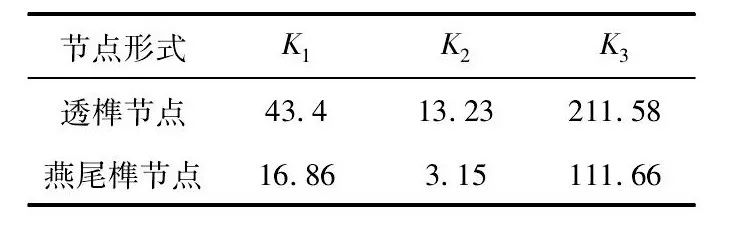
式中，M为节点弯矩，θ 为节点转角，R为相关系数，其中M =1. 4kNm和M = -1. 09kNm是曲线的上下渐近线。以上拟合公式符合榫卯节点的刚度增加和退化规律，并能较好的反映榫卯节点的转动刚度特性。

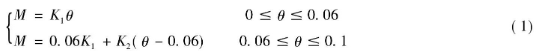
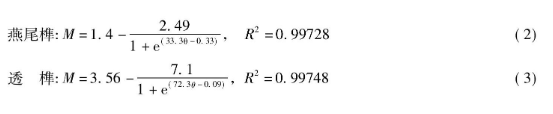
此外，淳庆以南方典型榫卯节点 (燕尾榫、十字箍头榫、半榫、馒头榫) 为目标，提出了考虑节点刚度退化阶段的简化三折线模型 (见图7) ，并计算了各阶段特征刚度［27］。

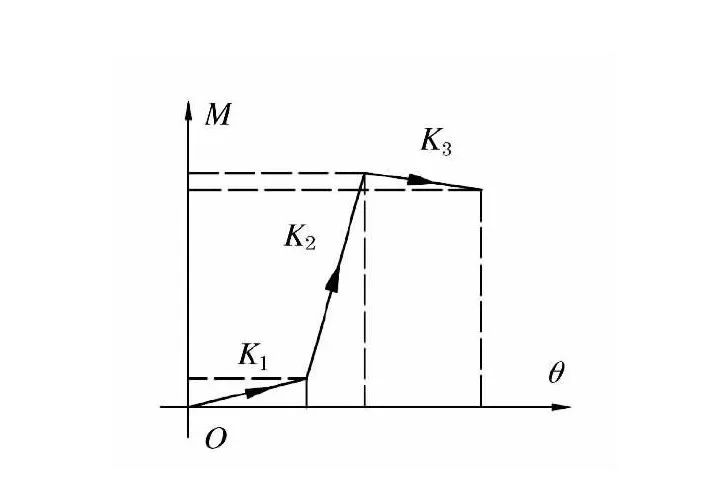
图 7 榫卯节点骨架曲线

以上恢复力模型，只能笼统的描述古木结构榫卯半刚性连接特性，不能描述榫卯尺寸等因素的影响，具有一定的局限性。杨艳华等利用最小二乘法对试验数据进行处理，得出榫头尺寸及卯孔对刚度影响的规律，建立了4参数幂函数弯矩- 转角的相关曲线模型［28］：

上式中，M为节点弯矩；r为卯口影响系数，E₀为虚拟初始弹性模量，l为榫头颈部转动惯性矩，l为榫头长度，θ 为节点转角，θ_u为参考塑性转角，θ_u= M_u/ R_kl，M_u为节点极限弯矩，R_ki为节点初始刚度，n为形状系数。该表达式可以描述榫卯连接尺寸的影响，更具有概括性，可直接应用于计算，给实际应用带来方便，并且与试验吻合的比较好。

由于榫卯连接中，榫头有一定的长度，榫卯之间的结构有一定的间隙，因此该连接并非刚接，也非铰接，而是表现为介于刚接和铰接之间的变刚性连接，因此计算分析时将该种类型的榫卯连接简化为变刚度单元加入有限元程序中进行分析［29］。

赵均海等［30 －31］在对西安古城墙箭楼结构抗震性能的计算分析研究中，用三维可变刚性节点单元 (半刚性单元) ，作为梁柱间的过渡性单元，加在梁单元的两端，通过采用改变刚度矩阵中的弯矩及其耦合项的方法来模拟接头的半刚性特性，进而分析具有该连接的梁柱结构。其特点为在单元刚度矩阵中引入3个参数r1，r2，r3来描述弯曲刚度折减后的杆单元刚度，其矩阵形式为

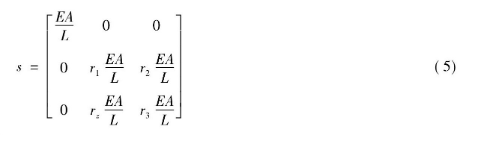
以上方法在计算西安东门城楼古建木结构地震特性分析中得到验证，计算了结构的固有频率，以及在地震作用下典型单元的轴力响应曲线和位移、加速度响应曲线。文献[32]还应用以上单元，建立西安鼓楼的三维有限元模型，进行了动力特性分，地震动时程分析和PUSHOVER分析，得到了鼓楼的自振特性和地震响应状况，较好地预测了鼓楼在水平荷载作用下的破坏过程及塑性发展阶段。

方东平、俞茂宏等［33 －36］对以上方法进行了进一步完善，他们利用现场实测和模型实验获得的结构自振频率的结果，使用Simplex方法反演推断半刚性节点单元的参数范围，推导出榫卯节点刚度，并进一步对西安北门箭楼动力特性进行了计算，取得了较好的效果。

高大峰等［37 －38］考虑了地震作用下榫、卯间接触摩擦行为，通过接触有限元法分析榫卯节点及其不同方向的刚度值，采用虚拟弹簧单元模拟榫卯连接的半刚性特征，并对其进行静力特性及动力特性分析。其采用接触单元conta174覆盖在榫头的表面，目标单元为targe170单元，二者形成接触对。采用这种方法可以较为准确地模拟榫卯连接分析榫卯结构特性，得出与实际相符的结果。

在采用以上方法对以西安化觉巷清真寺内木牌楼的抗震性能分析中，确认了榫卯连接和铺作层斗栱连接的摩擦滑移消耗了地震的部分能量，使传至顶层的地震激励效应削弱，减小了地震的破坏强度。同时，还发现榫卯连接的耗能减震作用随着地震作用的增强也逐渐加强，并认为榫卯连接具有“遇强则强”的智能减震特点。

董益平等［6］、仓盛等［39］和竺润祥等［40］采用接触问题的相关理论对古建筑木结构直榫节点进行了分析，在基本假设范围内给出了接触边界条件，并从虚功原理出发推导了接触有限元方程。为实现接触问题的有限元求解，对求解方法进行了理论上的讨论，就接触问题的虚杆全量型有限元解法作了说明，给出了计算框图。通过假设，将直榫刚度简化为抗压刚度k₁及抗扭刚度k₂。在理论分析的基础上，以保国寺大殿为例进行了直榫连接计算及结构静力计算，采用接触问题的有限元求解方法，获得了直榫的k₁及k₂值，利用相应的计算结果，分析了大殿结构整体北倾的原因。

此外，隋允康等［41］在分析应县木塔残损状况时，探讨了榫卯节点的力学特性，建立了便于分析计算的榫、卯有限元模型，利用MSC有限元分析软件得到数值计算结果，与试验结果模型相对比，采用响应面方法和优化迭代方法通过MATLAB和C + + 语言编程，得到了榫、卯半刚性单元的参数值，进而对改进的应县木塔模型进行分析，使复杂的摩擦变形问题得到简化。

对历次地震中木结构古建筑的震害调查表明：在地震作用下，榫头在绕卯口转动过程中脱离卯口，产生脱榫，削弱了梁柱之间的联系，是造成结构发生损坏甚至倾覆的重要原因。经过加固的榫卯节点，在地震中发生拔榫现象的比例反而较少［42 －45］。

我国传统上多采用铁件拉结的方法加固古建筑榫卯节点，这种方法虽能在一定程度上提高节点抗震性能，但存在对木构件的破坏和加固措施“不可逆”等弊病。因此，改善铁件加固性能措施［46］以及采用FRP等新材料的加固方法，是近年来的研究热点。

铁件加固

我国部分地区传统上有采用马口铁加固榫卯节点的做法。马口铁一般是将采用光圆钢筋两端做成直钩后钉入榫卯节点，以增加节点及构架的强度和刚度，提高其整体性。试验表明，马口铁对榫卯节点的约束，在一定程度上可以减小节点拔榫量，提高构架的侧移刚度及承载力。加固后的构架刚度退化不明显，变形能力较强，但是耗能能力较加固前有所减弱［47 －48］。

姚侃等［47］在文献中提出一种采用Q235扁钢加固榫卯节点的方法，并通过振动台试验对模型加固前后的抗震性能进行了对比。加固后结构刚度略有提高，但结构自振频率变化不大；加固后结构阻尼比显著提高，榫卯结构耗能转变为主要依靠扁钢屈服后塑性变形耗能，有效阻止了结构榫卯节点的破坏。

周乾、闫维明等［49 －53］设计出一种新型钢构件加固装置 (见图8) ，并开展了比较详细的试验研究。

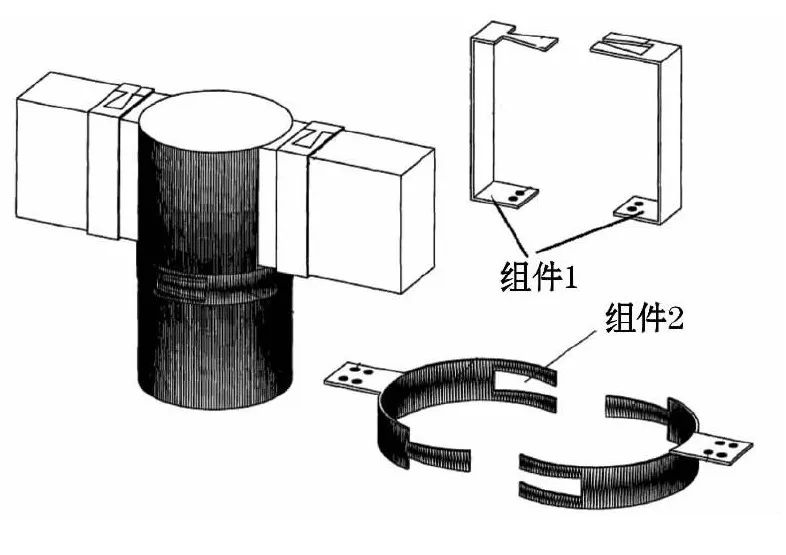
图8钢构件加固装置

这种新型钢构件加固装置能够有效约束节点转动，试验后节点拔榫量较加固前可降低60%，且节点的承载能力可提高至未加固节点的2. 5倍。加固后，节点滞回曲线的形状在加载初期为弓形，随着节点转角增大，形状转变为Z形，由于钢构件的约束作用，曲线在平衡位置的捏拢效应不明显，滞回环表现为中间位置比未加固节点饱满而两端比未加固节点捏缩。由于钢构件对节点变形的约束作用，使得钢构架加固节点耗能能力大于加固前。节点的延性系数变化不大，且远大于钢筋混凝土节点相关值。

FRP加固

纤维复合材料 (FRP) ，具有抗拉强度高，自重轻，耐腐蚀好，裁剪方便等优点，并在钢结构，钢筋混凝土结构等结构体系中得到了深入研究。利用它来包裹于榫卯节点区域以加固节点，即可约束节点拔榫，又可以增加了节点抗弯和抗剪能力，目前使用的加固材料主要为碳纤维 (CFRP) 和玄武岩纤维 (BFRP) 两种。

薛建阳等［54 －56］和周乾等［57 －58］等分别通过对采用CFRP材料加固节点的木构架分别开展了拟静力试验和振动台试验。加固构件拟静力试验的滞回曲线为梭形，滞回曲线比较饱满，曲线在平衡位置的捏拢效应不明显，在控制位移处的下降没有未加固节点明显，而且初始的刚度要比未加固构架的刚度大。加固构架的强度要高于未加固构架，加固构架承受的最大荷载与未加固构架承受的最大荷载大体相当。

两个课题组研究结果的差异在于，薛建阳等认为加固措施提高了塑性变形性能，构件延性系数要高于未加固构件的延性系数，且通过振动台试验表明，古代木构建筑榫卯节点经碳纤维布加固后，结构仍然具有良好的耗能减震能力，模型的自振周期和阻尼比随着地震激励的增加而增加，CFRP加固模型属于长周期低频率结构，且阻尼耗能能力强。周乾等研究结果表明，CFRP布加固节点后，构架的延性系数变化不大，并且由于CFRP布对节点对榫卯产生约束作用，节点的转动受到限制，榫头与卯口之间相对滑移距离减小，因而影响摩擦耗能能力减弱，构架的耗能能力有所略下降。

图 9 CFRP 加固节点

通过分析梁课题组的研究数据，之所以出现以上差异，可能是由于两方面的原因：一方面在于榫卯节点试件的加工误差，木质材料的性能差异以及木材本身的干裂和疤痕等影响了试验结果；另一方面，CFRP布粘贴方式和粘贴层数等的差异也是影响结果的重要原因。

法冠喆等［59］，王全凤等［60］对采用BFRP加固的榫卯节点拟静力试验表明，采用BFRP加固榫卯节点的滞回曲线比未加固榫卯节点的滞回曲线图更趋饱满，滞回环而积很大。各试件的刚度随加固层数的增加得到较大提高，加固后节点仍然具有非常好的变形性能。

由于选择的加固材料和加固方法的差异，加固效果也存在显著差别。综合分析不同加固方法的结果和数据，可以得出以下结论：

(1) 采用马口铁加固能够获得较好的整体性，减少节点拔榫量。加固后节点均有较好的耗能性能和变形能力，但对节点承载能力和刚度提高不大。

(2) 采用钢构件加固可有效提高构架的承载能力和刚度，加固后节点刚度退化不明显，且加固后的构架有较好的耗能能力和变形能力。

(3) 采用CFRP加固能够显著提高节点的承载力和刚度。但加固后对节点耗能能力的影响不同研究结果仍有差异。

尽管对木结构古建筑榫卯节点的抗震性能研究已经取得了大量的成果，但由于其在材质特征、结构构造、力学性能等方面的复杂性以及抗震设计的特殊性，目前研究仍旧处于初步阶段，没有形成统一的理论方法，尚存在许多问题需要进一步深入开展研究。

存在问题

(1) 现有的研究成果，主要为定性变化规律，还缺乏采用定量计算方法。榫卯节点构造复杂，在受外荷载作用过程中，节点经历了复杂的积压、摩擦、滑移等过程，榫头与卯口之间存在有不断变化的压、弯、剪、扭合摩擦力的作用。各种作用又受到材料的性能，榫头与卯口之间的缝隙，节点构造类型等多方面的影响。因此，基于现有研究数据还很难给出能准确计算节点抗震性能的定量计算方法。

(2) 综合比较不同学者的研究数据可以发现，不同学者的试验结果相差较大。即使是同一课题组度不同试件，其结果也有显著差异。其原因在于一方面，木材本身为生物质材料，不同树种之间材料性能差异很大，即使是同一树种，不同年代，不同成长地域等均会显著影响其材料性能，进而造成实验结果的差异；另一方面，节点的加工误差，木材蠕变、开裂、疤痕等也会对结果造成显著影响。

(3) 木材具有较高的变形能力，并且节点能够承受很大的转动和滑移变形。因而木构架发生很大水平为以后仍具有一定的刚度与承载能力，这一点与现代结构有显著差异。基于以上原因，试验过程中由于作动器臂长的限制，最大加载位移难以使得结构发生真正的破坏，试验结果的准确性有待验证。

(4) 大型有限元程序的发展，为我们分析木结构古建筑的抗震性能提供了重要手段。对于榫卯节点，尽管已经提出多种计算模型模拟节点工作状态，但目前仍缺乏一种通用性较强，且应用简便的方法。

(5) 由于使用年代久远，现存古建筑大部分属于带病工作，榫卯节点存在有拔榫、腐蚀、虫蛀等各种残损状态。对于不同残损状态榫卯节点的抗震性能研究，目前仍属于空白。

研究建议

(1) 针对古建筑木结构榫卯节点的复杂性和试验结果的离散性，应当深入探讨节点抗震性能试验的标准化问题，应当使试验方法、材料性能、节点构造和试件加工等尽量统一或者采取统一的衡量标准，使试验结果具有可比性。同时，应当继续深入开展不同节点的抗震性能试验，积累数据。

(2) 由于古建筑木结构独特的结构特点，榫卯节点的特殊性能，使得已经成熟的现代建筑结构动力计算理论难以适用于古建筑木结构，必须尽快建立科学合理的榫卯节点抗震性能定量计算方法和适合于古建筑木结构的动力计算理论。

(3) 应加强实地调查，明确古建筑木结构在材料性能、节点变形及构件截面削弱等方面的残损类型和残损规律，尽快开展残损节点抗震性能评估理论研究，建立起残损节点抗震性能计算方法。

(4) 针对古建筑木结构建筑物的修缮加固，应当进一步开展榫卯节点加固方法研究，优化古建筑木结构加榫卯节点固技术，建立面向结构性能的加固方法和计算设计理论。